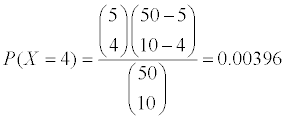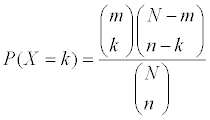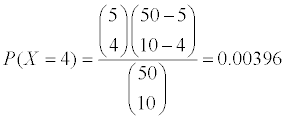- Η υπεργεωμετρική κατανομή είναι μια διακριτή συνάρτηση κατανομής τυχαίας μεταβλητής. Περιγράφει ένα τυχαίο πείραμα με δυο πιθανά αποτελέσματα (επιτυχία - αποτυχία) σε πεπερασμένο πληθυσμό που επαναλαμβάνεται n φορές χωρίς επεναφορά.
- Η κατανομή γίνεται εύκολα κατανοητή με την περιγραφή της μέσω ενός μοντέλλου με κάλπεις: Θεωρούμε μια κάλπη με m λευκές μπάλες (επιτυχίες) και Ν-m μαύρες (αποτυχίες). Από την κάλπη εκλέγουμε χωρίς επαναφορά n μπάλες. Η υπεργεωμετρική κατανομή μας δίνει την πιθανότητα οι k από αυτές να είναι λευκές. Η αντίστοιχη πιθανότητα είναι:
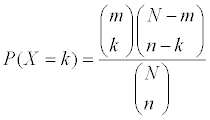
- m= Αριθμός επιτυχιών στον πληθυσμό
- Ν= Το μέγεθος του πληθυσμού
- n= Αριθμός στοιχείων που εκλέγονται τυχαία χωρίς επανάθεση
- k= Ο αριθμός των επιτυχιών που θέλουμε να ελέγξουμε εάν υπάρχει στο δείγμα
Παράδειγμα :
Φανταστείεότι έχουμε ένα καλάθι με 5 μπάλες άσπρες και 45 μαύρες (50 στο σύνολο). Επιλέγουμε τυχαία 10 μπάλες (χωρίς επανάθεση) και το ερώτημα είναι το εξής : Και θέτουμε το ερώτημα:
Ποια είναι η πιθανότητα ακριβώς οι 4 (από τις 10 ) να είναι άσπρες μπάλες?
Η απάντηση δίνεται από τον παρακάτω τύπο :